1) Teoría de conjuntos (ZF)
Este será uno de nuestros primeros acercamientos a la teoría de conjuntos desde la axiomática de Zermelo-Frankel (ZF), en un principio veremos una pequeña motivación del por que esta misma ha sido tan importante y trabajada por grandes maestros de las matemáticas, así en esta serie de post comentaremos y compararemos ZF con otras axiomáticas y veremos el por qué esta parece ser una de las más estandares en el mundo de las matemáticas.
Teoría de Conjuntos Axiomas Construcción
Este será uno de nuestros primeros acercamientos a la teoría de conjuntos desde la axiomática de Zermelo-Frankel (ZF), en un principio veremos una pequeña motivación del por que esta misma ha sido tan importante y trabajada por grandes maestros de las matemáticas, así en esta serie de post comentaremos y compararemos ZF con otras axiomáticas y veremos el por qué esta parece ser una de las más estandares en el mundo de las matemáticas.
Este es uno de los primeros resultados en teoría analítica de números, veremos una prueba sencilla de este y por qué implica que los primos son infinitos.
Aquí veremos una de las aplicaciones más populares de la teoría de números sobre la criptografía y la seguridad de nuestros datos.
¿Como podemos calcular el máximo común divisor de 2 enteros si no conocemos su expresión en factores primos?
Esta ecuación diofantica no tiene soluciones no triviales y veremos que probar esto es equivalente a probar que la ecuación \(x^4+y^4=z^4\) no tiene soluciones no triviales también. Además que \(x^n+y^n=z^n\) no tiene soluciones no triviales si \(n\) es una potencia de \(2\) mayor que \(2\).
El teorema chino del Residuo y solución de sistemas de congruencias
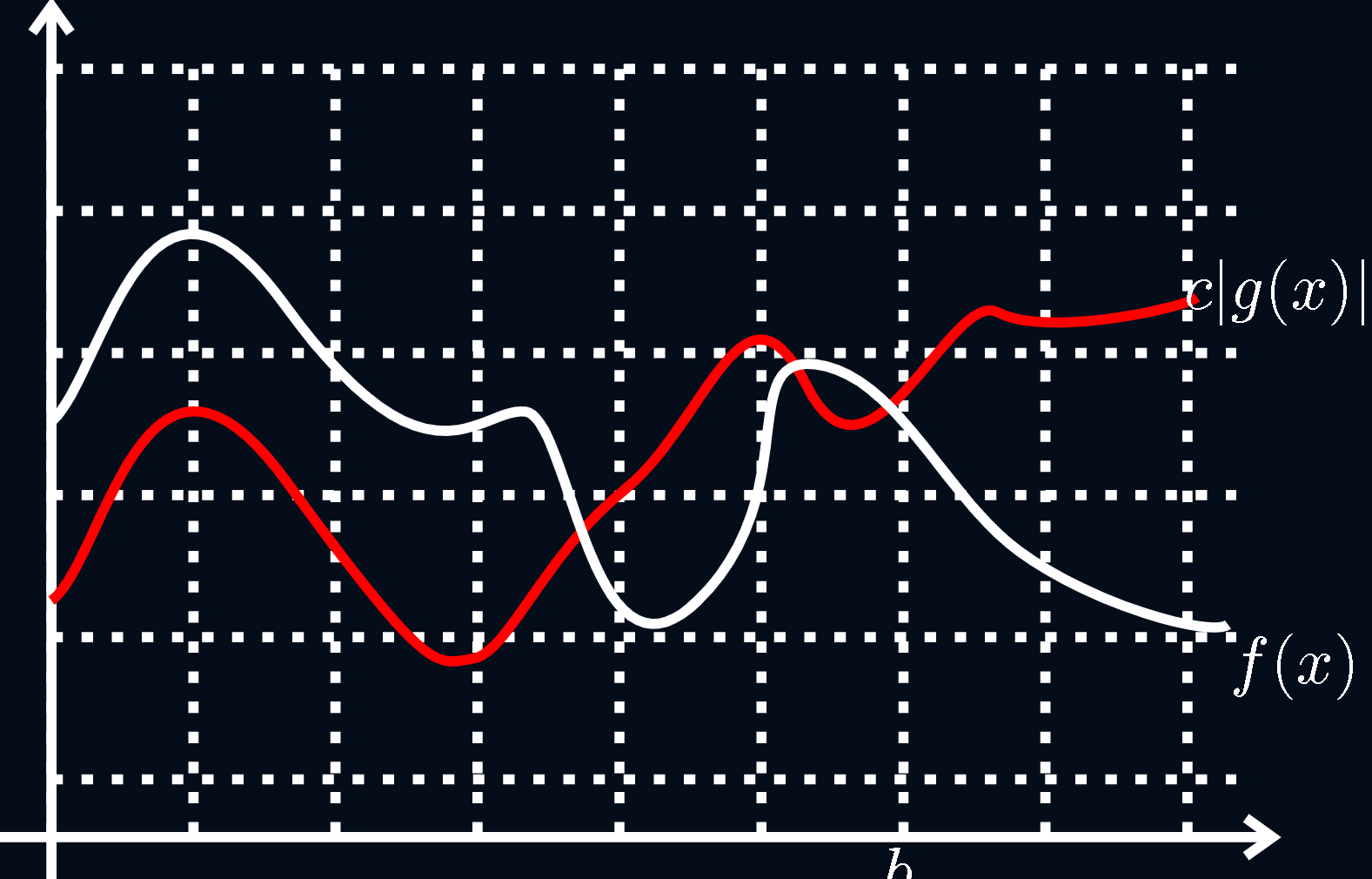Encontrar algoritmos eficientes para hacer todo tipo de tareas es algo muy complicado y a esto se dedican muchos matemáticos. Así mismo es importante entender que tanto tiempo u operaciones deben realizar nuestros algoritmos para realizar distintas tareas, por consiguiente la notación O grande es importante de entender, ya que esta nos permitirá acotar el tiempo de ejecución de nuestro algoritmo para algún \(n\) arbitrario.