La divergencia de \(\sum_{p \in \mathcal{P}}\dfrac{1}{p}\)
Este es uno de los primeros resultados en teoría analítica de números, veremos una prueba sencilla de este y por qué implica que los primos son infinitos.
Teoría de Números Teoría Analítica de Números Este es uno de los primeros resultados en teoría analítica de números, veremos una prueba sencilla de este y por qué implica que los primos son infinitos.
Este es uno de los primeros resultados en teoría analítica de números, veremos una prueba sencilla de este y por qué implica que los primos son infinitos.
 Aquí veremos una de las aplicaciones más populares de la teoría de números sobre la criptografía y la seguridad de nuestros datos.
Aquí veremos una de las aplicaciones más populares de la teoría de números sobre la criptografía y la seguridad de nuestros datos.
 ¿Como podemos calcular el máximo común divisor de 2 enteros si no conocemos su expresión en factores primos?
¿Como podemos calcular el máximo común divisor de 2 enteros si no conocemos su expresión en factores primos?
 Esta ecuación diofantica no tiene soluciones no triviales y veremos que probar esto es equivalente a probar que la ecuación \(x^4+y^4=z^4\) no tiene soluciones no triviales también. Además que \(x^n+y^n=z^n\) no tiene soluciones no triviales si \(n\) es una potencia de \(2\) mayor que \(2\).
Esta ecuación diofantica no tiene soluciones no triviales y veremos que probar esto es equivalente a probar que la ecuación \(x^4+y^4=z^4\) no tiene soluciones no triviales también. Además que \(x^n+y^n=z^n\) no tiene soluciones no triviales si \(n\) es una potencia de \(2\) mayor que \(2\).
 El teorema chino del Residuo y solución de sistemas de congruencias
El teorema chino del Residuo y solución de sistemas de congruencias
 ‘La teoría de números moderna comenzó con el descubrimiento de la ley de reciprocidad cuadrática’- Hecke ‘Ocupado con otro trabajo me encontré con una verdad aritmética extraordinaria. Como la consideré, muy bella en si misma, concentré en ella todos mis esfuerzos para entender los principios de los cuales dependía y para obtener una prueba rigurosa.’ - Gauss
‘La teoría de números moderna comenzó con el descubrimiento de la ley de reciprocidad cuadrática’- Hecke ‘Ocupado con otro trabajo me encontré con una verdad aritmética extraordinaria. Como la consideré, muy bella en si misma, concentré en ella todos mis esfuerzos para entender los principios de los cuales dependía y para obtener una prueba rigurosa.’ - Gauss
 En álgebra se estudian detalladamente las soluciones de ecuaciones polinómicas, de forma análoga aquí estudiaremos las congruencias polinómicas con coeficientes en los enteros
En álgebra se estudian detalladamente las soluciones de ecuaciones polinómicas, de forma análoga aquí estudiaremos las congruencias polinómicas con coeficientes en los enteros
 Aquí veremos una introducción a la aritmética modular y su fundamentación con base a las congruencias, definiremos estos conceptos y veremos un par de resultados
Aquí veremos una introducción a la aritmética modular y su fundamentación con base a las congruencias, definiremos estos conceptos y veremos un par de resultados
 En álgebra es usual preguntarse por soluciones a ciertos problemas restringiendo el conjunto de salida de las mismas, las ecuaciones diofánticas son un caso más en el que esto ocurre y veremos como estas engloban varios de los problemas más complejos de la teoría de números
En álgebra es usual preguntarse por soluciones a ciertos problemas restringiendo el conjunto de salida de las mismas, las ecuaciones diofánticas son un caso más en el que esto ocurre y veremos como estas engloban varios de los problemas más complejos de la teoría de números
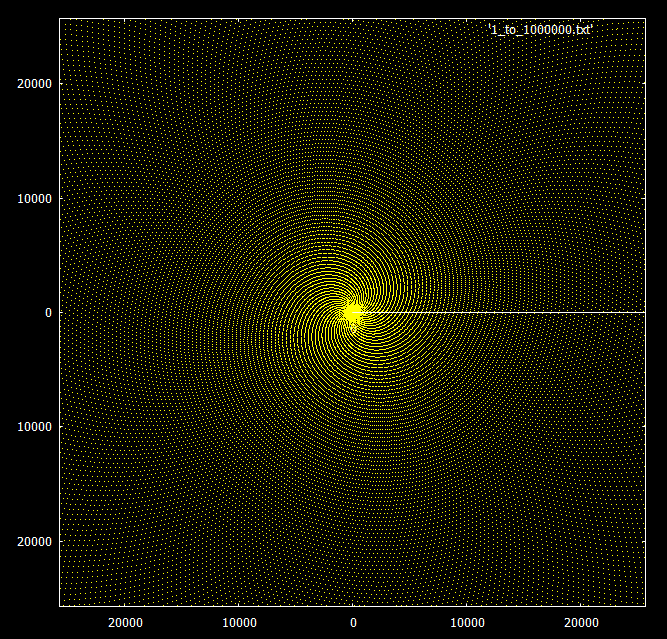 Al estudiar la distribución de los números primos es natural preguntarnos si es posible que un polinomio nos proporcione una formula para determinar el siguiente, aquí veremos que al menos en polinomios de una variable esto es imposible.
Al estudiar la distribución de los números primos es natural preguntarnos si es posible que un polinomio nos proporcione una formula para determinar el siguiente, aquí veremos que al menos en polinomios de una variable esto es imposible.
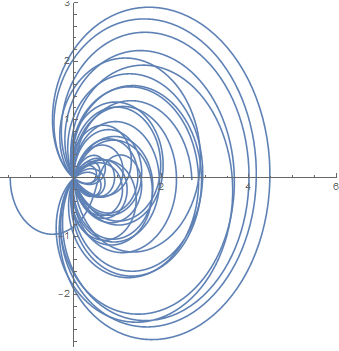 Al estudiar la función zeta de Riemann es natural preguntarnos su relación con los números primos y esta es quizás unas de las primeras que podemos encontrar, el producto de Euler además es uno de los primeros teoremas que relacionan el análisis con la teoría de números.
Al estudiar la función zeta de Riemann es natural preguntarnos su relación con los números primos y esta es quizás unas de las primeras que podemos encontrar, el producto de Euler además es uno de los primeros teoremas que relacionan el análisis con la teoría de números.
 El teorema de pitágoras es uno de los más conocidos de toda la matemática, además tiene una gran cantidad de pruebas, hoy veremos dos de ellas, una de ellas propuesta por un presidente de los EE.UU.
El teorema de pitágoras es uno de los más conocidos de toda la matemática, además tiene una gran cantidad de pruebas, hoy veremos dos de ellas, una de ellas propuesta por un presidente de los EE.UU.
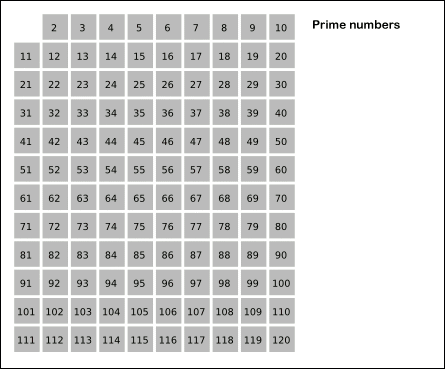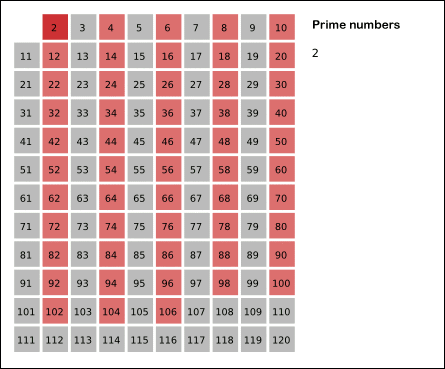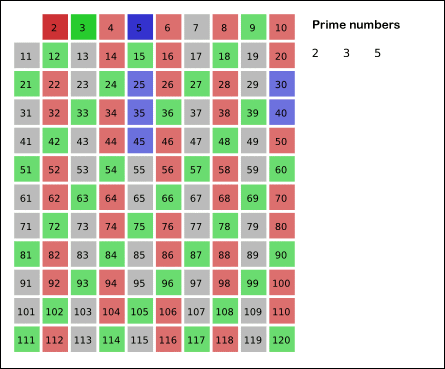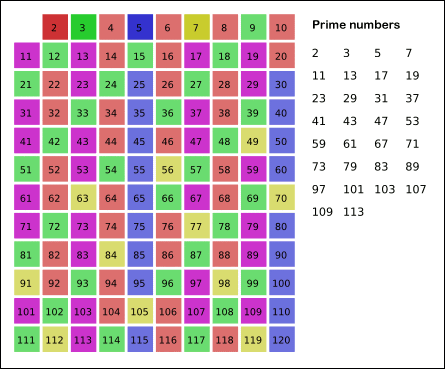 Eratóstenes de Cirene, matemático griego, desarrollo alrededor de los años 200 a.C un algoritmo que nos permite identificar los números primos menores a un \(n\) dado. Veremos como funciona este algoritmo, daremos un par de detaller del mismo, y por otro lado expondremos una relación entre este algoritmo y el teorema de Dirichlet.
Eratóstenes de Cirene, matemático griego, desarrollo alrededor de los años 200 a.C un algoritmo que nos permite identificar los números primos menores a un \(n\) dado. Veremos como funciona este algoritmo, daremos un par de detaller del mismo, y por otro lado expondremos una relación entre este algoritmo y el teorema de Dirichlet.
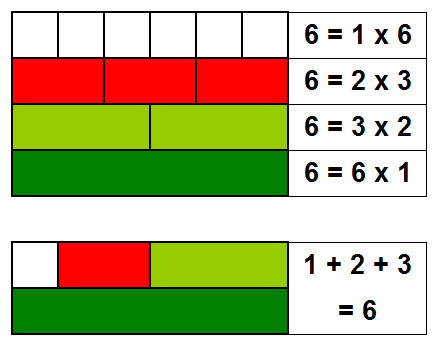 Euler demostró además que todo número perfecto par es justamente de la forma \(2^{p-1}•(2^{p} - 1)\), luego la relación entre estos dos conjuntos de números enteros es justamente biyectiva, aún no podemos descartar la existencia de un números perfecto impar pero sabemos que si existe debe ser mayor que \(10^{300}\).
Euler demostró además que todo número perfecto par es justamente de la forma \(2^{p-1}•(2^{p} - 1)\), luego la relación entre estos dos conjuntos de números enteros es justamente biyectiva, aún no podemos descartar la existencia de un números perfecto impar pero sabemos que si existe debe ser mayor que \(10^{300}\).
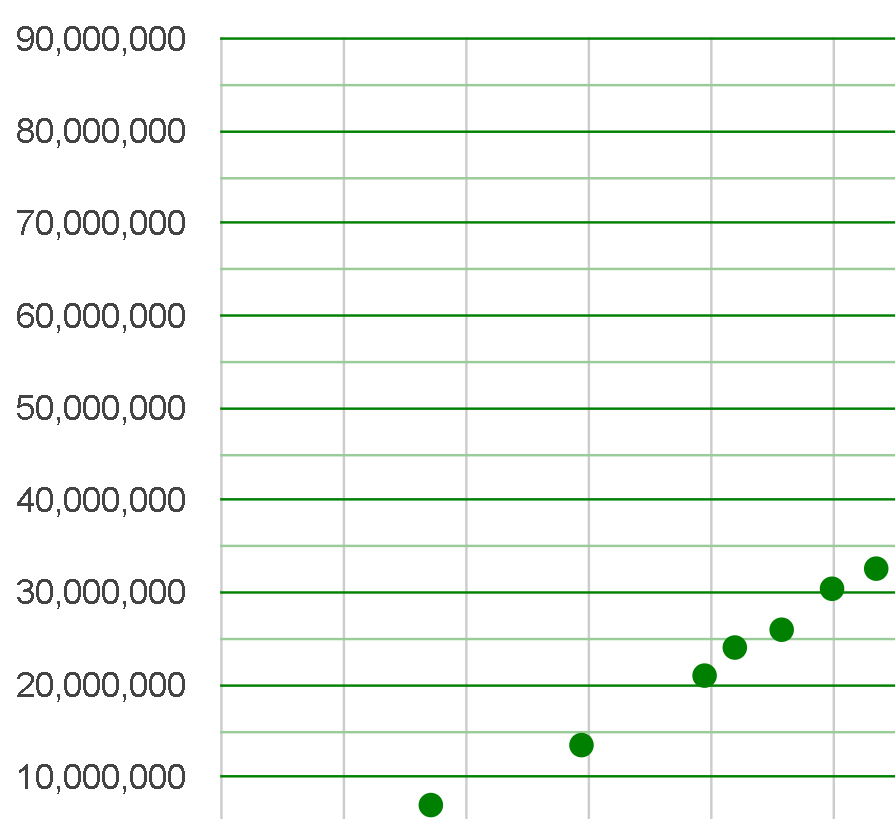 El 7 de diciembre de 2018 fue descubierto el que actualmente es el número primo más grande conocido, con más de 24 millones de cifras este gigantezco número es un primo de Mersenne
El 7 de diciembre de 2018 fue descubierto el que actualmente es el número primo más grande conocido, con más de 24 millones de cifras este gigantezco número es un primo de Mersenne
 Leonhard Euler demostró aproximadamente en 1772 que 2.147.483.647 es un numero primo y le mando una carta a Daniel Bernoulli informandole de su prueba, ¿Cómo fue que lo hizo con las limitaciones de su epoca para realizar cálculos?
Leonhard Euler demostró aproximadamente en 1772 que 2.147.483.647 es un numero primo y le mando una carta a Daniel Bernoulli informandole de su prueba, ¿Cómo fue que lo hizo con las limitaciones de su epoca para realizar cálculos?
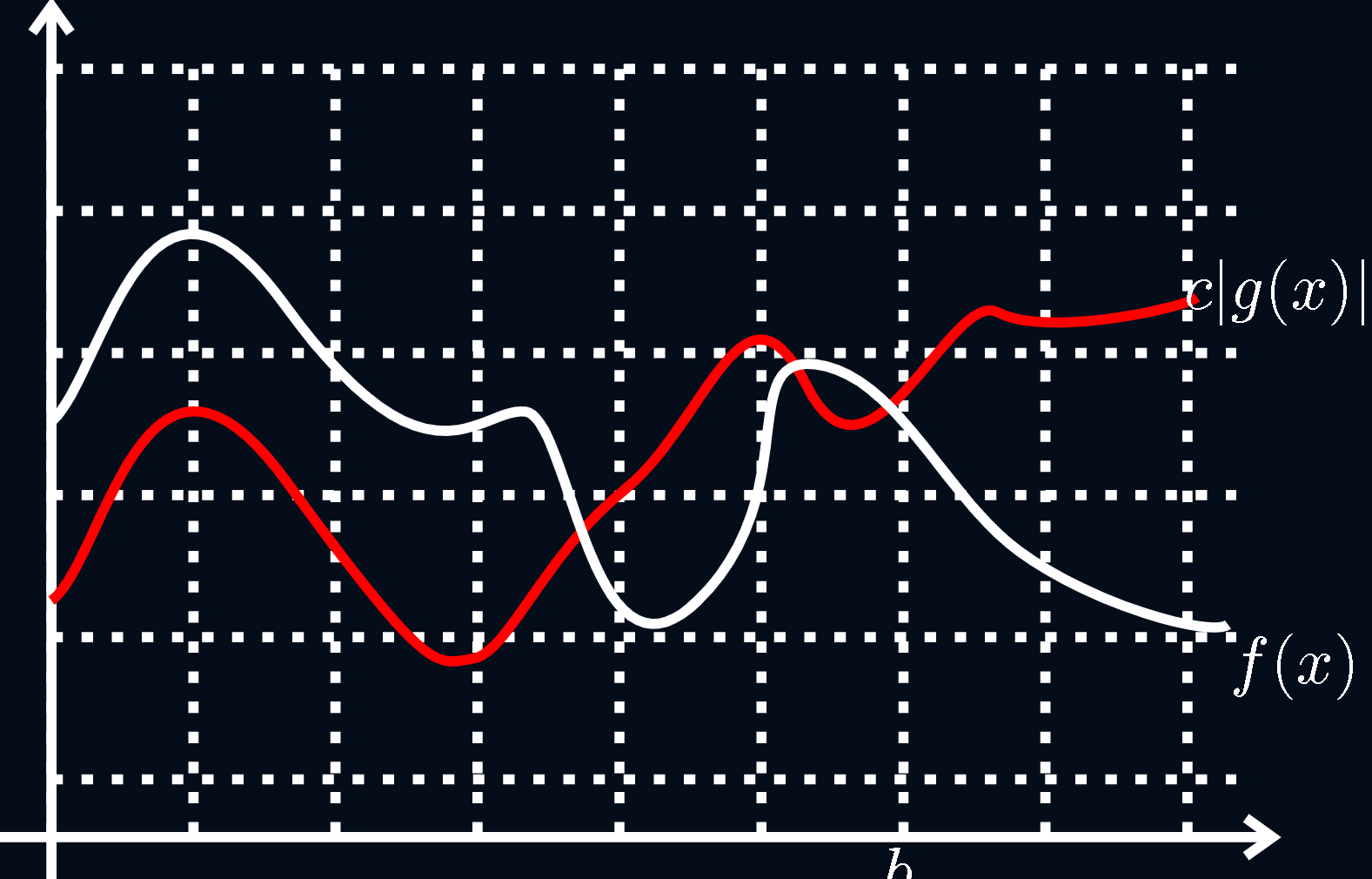 Encontrar algoritmos eficientes para hacer todo tipo de tareas es algo muy complicado y a esto se dedican muchos matemáticos. Así mismo es importante entender que tanto tiempo u operaciones deben realizar nuestros algoritmos para realizar distintas tareas, por consiguiente la notación O grande es importante de entender, ya que esta nos permitirá acotar el tiempo de ejecución de nuestro algoritmo para algún \(n\) arbitrario.
Encontrar algoritmos eficientes para hacer todo tipo de tareas es algo muy complicado y a esto se dedican muchos matemáticos. Así mismo es importante entender que tanto tiempo u operaciones deben realizar nuestros algoritmos para realizar distintas tareas, por consiguiente la notación O grande es importante de entender, ya que esta nos permitirá acotar el tiempo de ejecución de nuestro algoritmo para algún \(n\) arbitrario.
 Abel fue un matemático Noruego que ha inspirado a muchos matemáticos, sus aportes se centran principalmente en el álgebra, sin embargo hoy veremos uno de sus aportes a la rama del análisis.
Abel fue un matemático Noruego que ha inspirado a muchos matemáticos, sus aportes se centran principalmente en el álgebra, sin embargo hoy veremos uno de sus aportes a la rama del análisis.
 Este será uno de nuestros primeros acercamientos a la teoría de conjuntos desde la axiomática de Zermelo-Frankel (ZF), en un principio veremos una pequeña motivación del por que esta misma ha sido tan importante y trabajada por grandes maestros de las matemáticas, así en esta serie de post comentaremos y compararemos ZF con otras axiomáticas y veremos el por qué esta parece ser una de las más estandares en el mundo de las matemáticas.
Este será uno de nuestros primeros acercamientos a la teoría de conjuntos desde la axiomática de Zermelo-Frankel (ZF), en un principio veremos una pequeña motivación del por que esta misma ha sido tan importante y trabajada por grandes maestros de las matemáticas, así en esta serie de post comentaremos y compararemos ZF con otras axiomáticas y veremos el por qué esta parece ser una de las más estandares en el mundo de las matemáticas.