Función phi de Euler
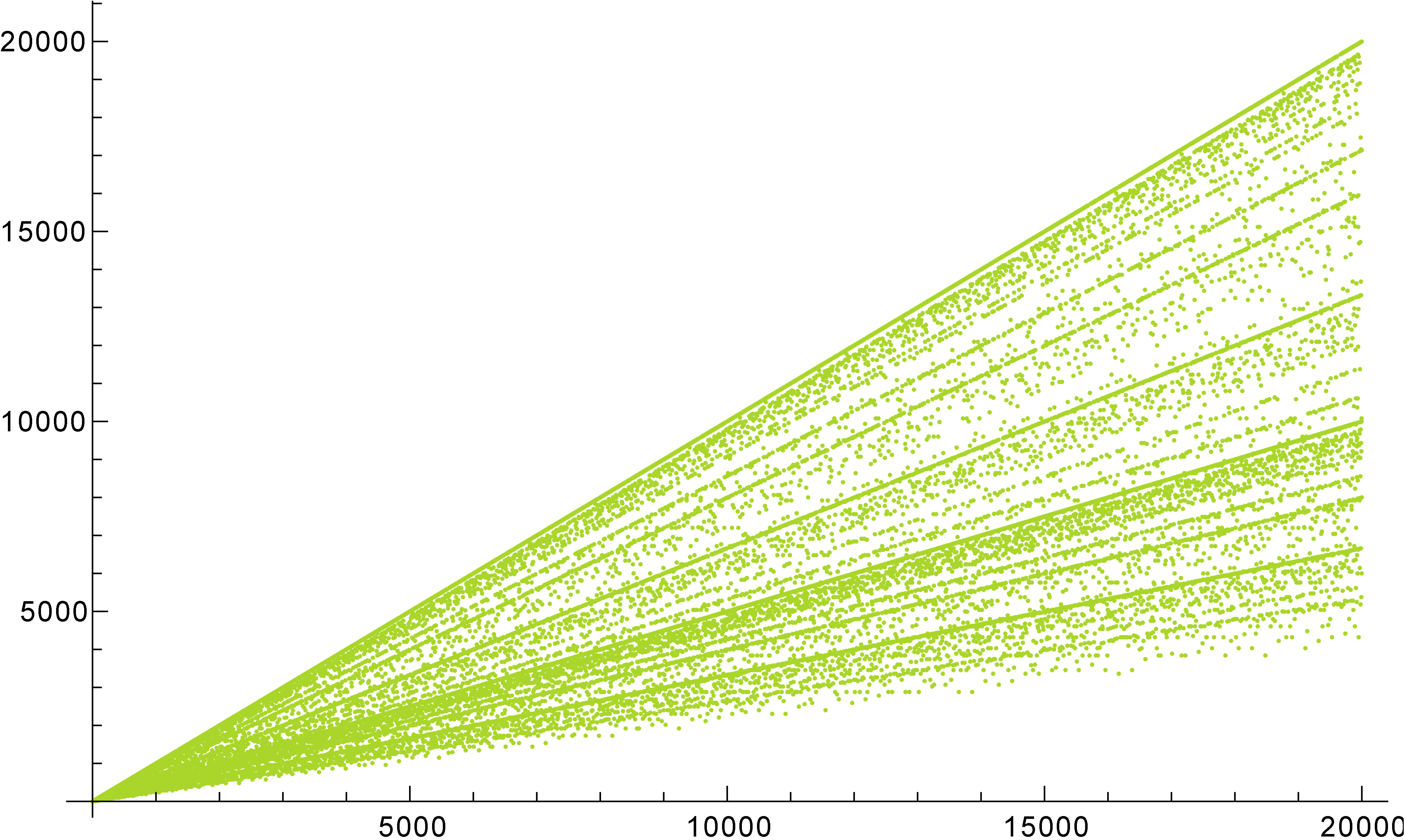
Veamos entonces la definición de la función.
Definición
Para cada entero positivo \(n\), definimos \(\Phi(n)\) como el número de enteros positivos menores o iguales que \(n\) que son primos relativos con \(n\).
\[\begin{array}{|r|r|r|r|r|r|r|r|r|r|r|} \hline n & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\ \hline \Phi(n) & 1 & 1 & 2 & 2 & 4 & 2 & 6 & 4 & 6 & 4 \\ \hline \end{array}\]Si observamos con detenimiento la gráfica nos damos cuenta que esta tiene una especie de “líneas”, la línea principal se debe a que \(\Phi(p)=p-1\) para todo $p$ primo, pero observamos más de una… Veamos una de las razones por las que esto ocurre Propiedades de \(\phi(n)\) :
- \[\Phi(p)=p-1\]
- \[\Phi\left(p^k\right)=(p-1) p^{k-1}\]
- Si m.c.d. \((m, n)=1\), entonces \(\Phi(m n)=\Phi(m) \Phi(n)\) A esto se le conoce como función multiplicativa (al menos en este caso \(\mathrm{xd}\) ), si además no fuera necesaria la condición de m.c.d \((m, n)=1\), entonces decimos que es completamente multiplicativa.
Antes de ver dos propiedades más veamos el Teorema Fundamental de la Aritmética.
Teorema fundamental de la aritmética:
Todo entero \(n>1\) o es primo o se puede representar de manera única como producto de primos.
\[n=\prod_{i=1}^k p_i^{n_i}\]donde \(n_i>0\) y \(p_i \neq p_j$ si $i \neq j\).
A esta representación del entero \(n\) la llamamos representación canónica.
- Si \(n=\prod_{i=1}^\kappa p_i^{n_i}\) es la representación canónica de un entero positivo \(n\), entonces.
Ahora sí veamos qué pasa con el resto de lineas en el gráfico.
Note que si fijamos \(q\), entonces \(\Phi(p \cdot q)=(p-1) \Phi(q)\) si \(p \nmid q\), entonces el conjunto de puntos
\[j=\{(p \cdot q, \Phi(q) \cdot(p-1)): p \nmid q\}\]está contenido en el gráfico y cae en la linea:
\[y=\Phi(q)\left(\frac{x}{q}-1\right)\]La última propiedad que veremos es la siguiente:
- Para todo entero positivo se tiene que \(\sum_{d \mid n} \Phi(d)=n\)
Y todas estas propiedades son muy útiles tanto para calcular \(\Phi(n)\) como para probar muchos teoremas en álgebra y teoría de números, por ejemplo los que vimos en el teorema chino del residuo, hagamos un ejemplo de cálculo.
\[\begin{aligned} \Phi(36) & =\Phi\left(3^2 2^2\right)=(3-1) 3^{(2-1)}(2-1) 2^{(2-1)} \\ & =2 \cdot 3 \cdot 1 \cdot 2 \\ & =12 \end{aligned}\]Y no hay una forma única de hacerlo.
\[\Phi(36)=\Phi\left(3^2 2^2\right)=36\left(1-\frac{1}{3}\right)\left(1-\frac{1}{2}\right)=12\]Ahora, muchas de estas funciones aritmética dependen de conocer la factorización del entero en cuestión lo cual es un problema y una bendición al tiempo, aunque el problema es para los que hacen álgebra computacional, los demás somos felices.
El siguiente post es de RSA, allí veremos para qué todo esto.