La criba de Eratóstenes.
Introducción
Vamos a conocer la criba de Eratóstenes, uno de los algoritmos más conocidos para obtener y listar números primos. Además veremos su relación con el teorema de Dirichlet.
Pseudocódigo
En un futuro presentaremos a qué nos referimos con esto de Complejidad e introduciremos la notación \(O\) grande.
La criba de Eratóstenes (Complejidad \(O(n\log{\log{n}})\))
Entrada: \(n\in\mathbb{N}\).
Algoritmo:
- Escriba todos los números naturales de \(2\) hasta \(n\).
- Tache todos los múltiplos de \(2\) hasta \(n\) a excepción de \(2\).
- A continuación busque el siguiente número que no se encuentre tachado, en este caso el \(3\), y tache todos los múltiplos de \(3\) hasta \(n\) a excepción de \(3\), luego repita este mismo procedimiento hasta que el último número tachado sea menor o igual a \(\sqrt{n}\) (la razón de esto la vimos en el post de división por tentativa #Probar si se puede dejar el hipervinculo).
Salida: Todos los números que no estén tachados son números primos.
Ejemplo
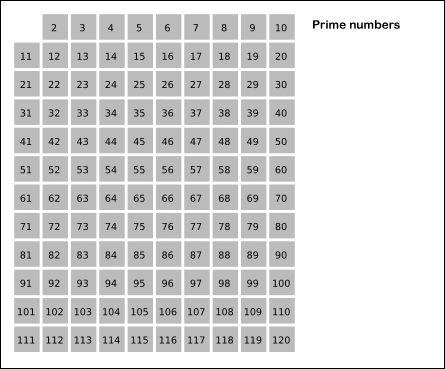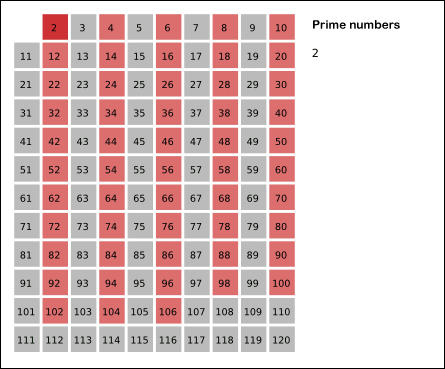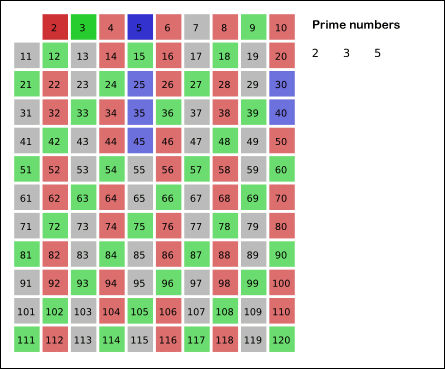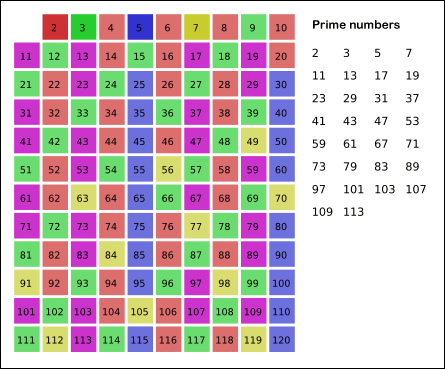
Supongamos que queremos encontrar los números primos menores que \(50\), debemos entonces aplicar el algoritmo con \(n=50\), gráficamente el resultado debería de ser el siguiente:
\[\begin{array}{cccccc} & 2 & 3 & \not4 & 5 & \not 6 \\ 7 & \not 8 & \not9 & \not10 & 11 & \not12 \\ 13 & \not14 & \not15 & \not16 & 17 & \not18 \\ 19 & \not20 & \not21 & \not22 & 23 & \not24 \\ \not25 & \not26 & \not27 & \not28 & 29 & \not30 \\ 31 & \not32 & \not33 & \not34 & \not35 & \not36 \\ 37 & \not38 & \not39 & \not40 & 41 & \not42 \\ 43 & \not44 & \not45 & \not46 & 47 & \not48 \\ \not49 & \not50 & & & & \end{array}\]Si verificamos el procedimiento por pasos podremos notar que el último número del cuál tomaremos múltiplos para tachar es el \(7\), esto es justamente porque \(7\leq \sqrt{50}\), en otras palabras, \(7^{2}=49 \leq 50\) y el \(50\) queda tachado al ser múltiplo de \(2\).
Además, si somos curiosos y observamos con detenimiento la gráfica notaremos que a excepción de \(2\) y \(3\) todos los números primos se encuentran en la primera y quinta columna, en nuestro caso, sabemos que los números de la primera columna son de la forma \(6k+1\) y los números de la quinta columna son de la forma \(6k+5\).
¡Nuevamente las matemáticas nos van a demostrar que las coincidencias no existen! Veamos porqué ocurre esto.
Teorema de Dirichlet
Si \(mcd(a,d)=1\) (Máximo común divisor de \(a\) y \(d\) es igual a \(1\)) con \(a,d\in\mathbb{Z}^{+}\), entonces hay un número infinito de primos de la forma \(a+dk\) con \(k\in\mathbb{Z}^{+}\).
En nuestro caso, como \(mcd(6,1)=1\), entonces tenemos que existen infinitos números primos de la forma \(6+k\). De la misma forma como \(mcd(6,5)=1\), entonces tenemos que existen infinitos números primos de la forma \(6+5k\).
Veamos de manera rápida porqué esto no ocurre para las demás columnas:
-
Suponga \(p\in\mathbb{N}\) como un número primo, luego si \(n=6+2k\), entonces \(p=2(3+k)\), CONTRADICCIÓN, ya que por hipótesis \(p\) es un número primo.
-
Suponga \(p\in\mathbb{N}\) como un número primo, luego si \(n=6+3k\), entonces \(p=3(2+k)\), CONTRADICCIÓN, ya que por hipótesis \(p\) es un número primo.
-
Suponga \(p\in\mathbb{N}\) como un número primo, luego si \(n=6+4k\), entonces \(p=2(3+2k)\), CONTRADICCIÓN, ya que por hipótesis \(p\) es un número primo.
-
Suponga \(p\in\mathbb{N}\) como un número primo, luego si \(n=6+6k\), entonces \(p=6(1+k)\), CONTRADICCIÓN, ya que por hipótesis \(p\) es un número primo.
Esto es equivalente a demostrar que todo número primo mayor o igual que \(5\) es de la forma \(6k+1\) o de la forma \(6k+5\), siendo esta la misma razón por la cuál los números primos aparecen en estas columnas. Por otro lado, este resultado se puede probar adaptando una demostración de Euclides, pero hemos visto como el teorema de Dirichlet generaliza esta situación.