Los números perfectos.
Se conocen actualmente 51 números perfectos y 51 primos de Mersenne, ¿es esto coincidencia?
Respuesta corta: no
Respuesta larga: noooooooooooooooooo
Veamos la relación entre estos dos interesantes conjuntos de números.
Definición
Sea \(n\) un entero positivo, decimos que \(n\) es un número perfecto si es igual a la suma de sus divisores (positivos) propios, es decir todos menos el propio número.
Ejemplo
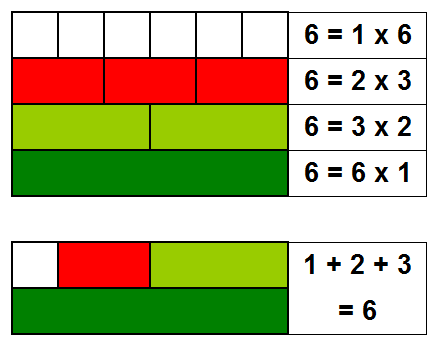
- 6 es divisible entre 1, también entre 2 y entre 3, por tanto 6 es un número perfecto ya que 1+2+3=6
Los cuatro primeros números perfectos son 6, 28, 496 y 8128, el quinto ya da un salto enorme ya que es 33550336.
Con esto nos hacemos la idea de que son números muy especiales y escasos, de hecho a día de hoy no se sabe si son infinitos, sin embargo el siguiente teorema nos da una manera de construirlos que además los relaciona con los primos de Mersenne (que tampoco se sabe si son infinitos).
Teorema
Sea \(n \in \mathbb{Z}\), si \(2^n-1\) es un primo de Mersenne, entonces \(\left(2^{n-1}\right) \cdot\left(2^n-1\right)\) es un número perfecto.
Podemos ver a partir de este teorema lo siguiente:
\(3=2^2-1\), es decir un primo de Mersenne, entonces \(\left(2^1\right) \cdot\left(2^2-1\right)=2 \cdot 3=6\), que sabemos que es un número perfecto.
Análogamente podemos ver que si \(n=3,2^3-1=7\), por lo tanto por el teorema anterior:
\(\left(2^2\right) \cdot\left(2^3-1\right)=4 \cdot 7=28\) y 28 es un número perfecto Por lo tanto, podemos ver que siempre que tengamos un primo de Mersenne podemos generar a partir de él un número perfecto.
Es increible como Euclides hace más de 2300 años logró demostrar esta relación, a partir de esto podemos ver una vez más que su legado trasciende mucho más allá de la geometría.
Algunos datos adicionales a considerar sobre los números perfectos es que todos los que se conocen son pares y no sabemos si existe uno impar, o si son infinitos, pero sabemos que si los primos de Mersenne lo son, esto implicaría que los números perfectos también y esto es justamente por el teorema que los relaciona.
Demostración:
Supongamos que \(2^n-1\) es primo, veamos que \(\left(2^{n-1}\right) \cdot\left(2^n-1\right)=N\) es un número perfecto.
Queremos ver que \(N\) es la suma de sus divisores menos él mismo, luego tenemos que por definición de \(\mathrm{N}\), la suma de sus divisores el producto de la suma de los divisores de \(2^{n-1}\) y \(2^n-1\).
Los divisores de \(2^{n-1}\) son \(1,2,4,8, \ldots, 2^{n-1}\), y tenemos que \(1+2+\ldots+2^{n-1}=2^n-1\).
Y como \(2^n-1\) es primo sus divisores son 1 y \(2^n-1\), por lo tanto la suma de sus divisores es \(2^n\).
Luego al hacer el producto de la suma de los divisores de \(2^{n-1}\) y \(2^n-1\) y restar el propio \(N\) (por definición de número perfecto) tenemos que:
\[\begin{aligned} \left(2^n\right) \cdot\left(2^n-1\right)-N & =\left(2^n\right) \cdot\left(2^n-1\right)-\left(2^{n-1}\right) \cdot\left(2^n-1\right) \\ & =\left(2^n-1\right) \cdot\left(2^{n-1}\right) \\ & =N \end{aligned}\]Luego es claro que \(\mathrm{N}\) es un número perfecto ya que la suma de sus divisores menos él mismo es justamente \(\mathrm{N}\).
\[\tag*{$\blacksquare$}\]