Los números primos de Mersenne
Teorema
Sea \(n \in \mathbb{Z}\), si \(2^n-1\) es primo, entonces \(n\) es primo.
Demostración:
Supongamos que \(n>1\) es un número compuesto, luego por el Teorema Fundamental de la Aritmética \(n=p \cdot q\), con \(p, q \in \mathbb{Z}\) y \(p, q>1\), sabemos que.
\[a^m-b^m=(a-b)\left(a^{m-1}+a^{m-2} b+\ldots+a b^{m-2}+b^{m-1}\right)\]Tomando \(a=2^p\) y \(m=q\) tenemos lo siguiente:
\[\begin{aligned} \left(2^p\right)^q-1 & =\left(2^p\right)^q-1^q \\ & =\left(2^p-1\right)\left(\left(2^p\right)^{q-1}+\left(2^p\right)^{q-2}+\ldots+2^p+1\right) \end{aligned}\]Y por la propiedad clausurativa en los enteros en cada caso, podemos garantizar que \(2^{p \cdot q}-1\) es compuesto, por tanto no es primo, lo cual es una contradicción, luego, es claro que \(n\) debe ser primo.
\[\tag*{$\blacksquare$}\]Nota
El recíproco es falso, que \(n\) sea primo, no implica que \(2^n-1\) sea primo, en caso de que lo sea se dice que es un primo de Mersenne.
Ejemplos
- \(2^2-1=3\) es un número primo (Mersenne)
- \(2^3-1=7\) es un número primo (Mersenne)
- \(2^5-1=31\) es un número primo (Mersenne)
- \(2^7-1=127\) es un número primo (Mersenne)
- \(2^{11}-1=2047\) no es un número primo
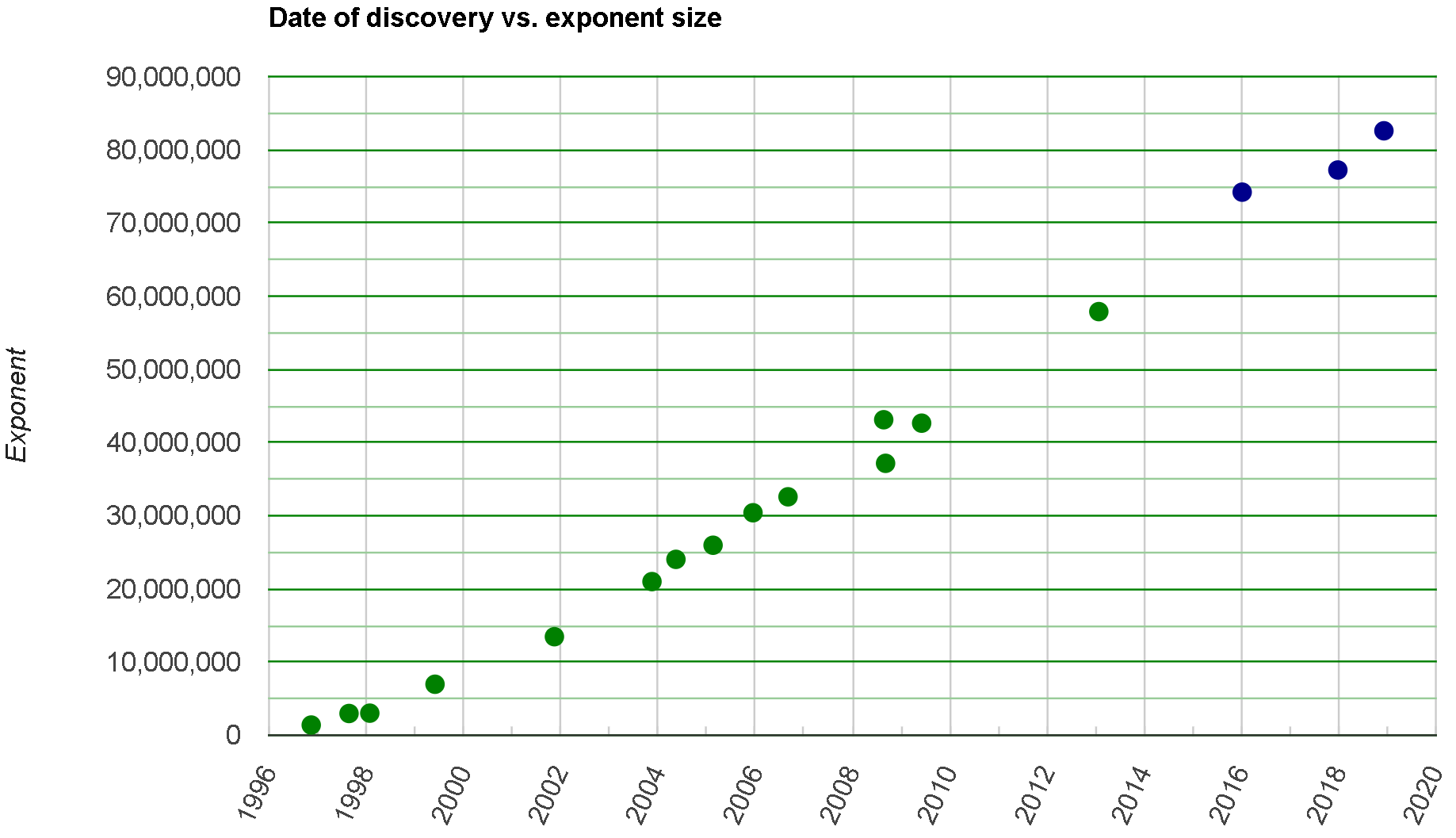
El primo de más de 24 millones de cifras mencionado al inicio es \(2^{82589933}-1\) denotado por \(M_{82589933}\)
Fue encontrado por Patrick Laroche, a traves de la GIMPS (Great Internet Mersenne Prime Search) y fue recompensado con 3000 dólares
El primo de Mersenne \(M_{57885161}\) tiene 17425170 cifras. Harían falta 13000 páginas para mostrar el número entero, con una letra de \(12 \mathrm{pt}\) y sin espacios.
Actualmente la EFF (Electronic Frontier Foundation) tiene una recompensa de \(150.000\) dólares para quien encuentre un primo de Mersenne de 100 millones de dígitos o más.
A día de hoy se conocen solo 51 primos de Mersenne y nadie ha demostrado aún que sean infinitos, por lo que al encontrar uno no sabremos si estamos ante el último de ellos.